«Элементы геометрии Клеро (Elemens de Geometrie de Clairaut)». Par M.Clairaut (математик)
Париж-Дюран, Королевской академии наук, Королевского общества в Лондоне, 1753 г., 1753 год
| Параметры книги! |
| переплет: подарочный, эксклюзивный; антикварное издание |
Описание книги
«Элементы геометрии Клеро (Elemens de Geometrie de Clairaut)». Par M.Clairaut (математик). 1753 год
Париж-Дюран, Королевской академии наук, Королевского общества в Лондоне, 1753 г.
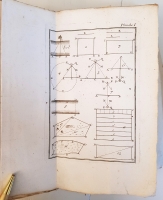
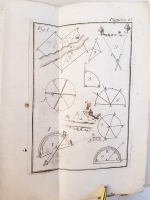
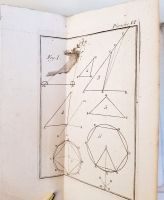
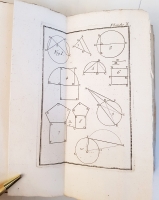
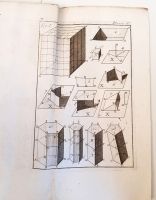
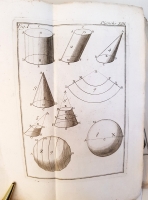
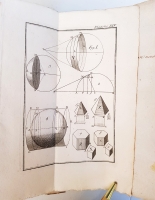
На французском языке. Необрезанный экземпляр. Без переплёта. 215 стр. текста с заставками и буквицами, и 14-ю гравюрами на отдельных листах.
Клеро Алексис Клод (7.5.1713-17. 5. 1765) - французский математик и астроном. Член Парижской Академии Наук (1831г.). Родился в Париже. Его отец Жан Батист Клеро был профессором математики в Париже и корреспондентом Академии Наук в Берлине. В 10 лет Клеро читал труды Г Лопиталя. В 12 с половиной лет написал работу по исследованиям алгебраических кривых 4-го порядка, одна из которых была, вероятно, тождественна с кампилой Евдокса. В 16 лет провел исследования кривых двоякой кривизны и в 18 лет опубликовал соответствующую работу, которая была первой попыткой изучения аналитической и дифференциальной геометрии пространственных кривых. В 18 лет был утвержден адъюнктом Парижской Академии Наук. В 1736г. участвовал в Лапландской экспедиции, целью которой было измерение дуги меридиана. На основе геодезической работы опубликованной в 1743г. книги "Теория фигуры Земли, основанная на началах гидростатики", в ней содержатся фундаментальные для высшей геодезии теоремы Клеро, устанавливающие связь между распределением силы тяжести на поверхности Земли и некоторыми параметрами, характеризующими ее форму и угловую скорость вращения. В этой книге поставлена общая задача о фигурах равновесия медленно вращающейся жидкости, впервые введены криволинейные интегралы.
В 1759г. Клеро исследовал движение кометы Галлея. В математическом анализе создал понятие полного дифференциала функции нескольких переменных и в 1739г. одновременно с Л. Эйлером, определил условие интегрируемости линейных дифференциальных форм от двух и трех переменных. На примере одного дифференциального уравнения 1-го порядка (уравнение Клеро) ввел понятие общего и особого решений дифференциального уравнения 1-го порядка. Нельзя не отметить также, что Клеро подготовил блестящие учебники «Начала геометрии» и «Начала алгебры».
Исследуя возмущения Солнца (1757г.), Клеро пришел к выводу, что любую четную функцию можно разложить в ряд. Но этот фундаментальный результат Клеро остался незамеченным. Клеро разработал аналитическую геометрию в пространстве. Клеро впервые предложил формулу тригонометрической интерполяции. Клеро и Эйлер являются создателями динамической теории относительного движения.
Клеро разработал новую теорию движения Луны (1751), провёл исследования фигуры Земли, доказав ряд фундаментальных для высшей геодезии теорем. На основе изучения движения кометы Галлея в 1759 определил момент её предстоящего прохождения через перигелий (погрешность была только около 1 мес). В механике создал динамическую теорию относительного движения (1742).
В 1754 Клеро был избран почётным членом Петербургской АН. Клеро неожиданно скончался в возрасте 52 лет в Париже, 17 мая 1765 года.
* * * Фотографии подарочной книги: "Элементы геометрии Клеро (Elemens de Geometrie de Clairaut)", Par M.Clairaut (математик), Париж-Дюран, Королевской академии наук, Королевского общества в Лондоне, 1753 г.: |